[논문 리뷰] DUSt3R: Geometric 3D Vision Made Easy

다양한 3D 프로젝트들을 하면서 3D에 관심이 많아진 참에 뉴스에서 해당 기술을 보게됐습니다. 네이버랩스 유럽이 발표한 기술인 DUST3R에 대해 리뷰해보려 합니다. (본인 공부 및 기록용)😁

github 링크 : DUSt3R github

논문 링크 : DUSt3R paper

논문 요약

카메라 포즈와 내부 파라미터를 모르는 이미지들로 DUSt3R은 pointmap을 생성하고 거기서 다양한 기하학적 정보들을 얻을 수 있습니다. (카메라 파라미터들, 픽셀 대응점들, 깊이맵, 3D reconstruction 등)

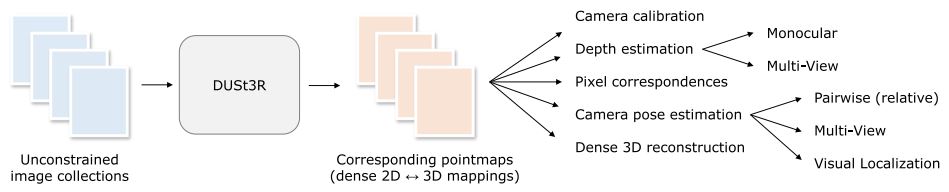
DUSt3R는 다양한 시점에서 촬영된 이미지로부터 3D 재구성을 수행하는 새로운 방법을 제안합니다. 일반적으로 다양한 시점에서 촬영된 이미지에서 3D 재구성을 하기 위해서는 카메라 내부/외부 파라미터가 필요합니다. (SfM, MVS 참고) DUSt3R은 카메라의 내부/외부 파라미터에 대한 사전 정보 없이도 3D 재구성을 가능하게 하며, 단일 이미지에서도 3D 재구성을 수행할 수 있습니다. 본 논문은 DUSt3R의 네트워크 구조와 학습 방법을 설명하고, 다양한 데이터셋에서의 성능을 통해 그 효용성을 입증하고 있습니다.

주요 Contribution

-'사전 정보 없이' 다중 뷰 재구성을 수행할 수 있는 새로운 접근 방식 제안
-'포인트맵 개념을 도입'하여 기하학적 제약을 없애고, 다양한 기하학적 정보를 학습할 수 있음
-Transformer Encoder-Decoder 기반으로 하며, 이미지 쌍에서 3D 포인트 맵을 예측
-다양한 데이터 셋에서 우수한 성능을 보이고, 특히 단일 이미지와 다중 이미지 재구성 모두에서 높은 정확도를 보임
    

주요 내용

문제 정의 및 접근 방식

전통적인 방법은(SfM, MVS 등) 카메라 파라미터를 먼저 추정해야 하며(Camera Calibration), 이는 복잡하고 시간이 많이 소요되는 작업이며, 오차가 발생할 가능성도 높습니다. 또한 고도로 기하학적 지식을 필요로 하며, 많은 계산을 요구합니다.

DUSt3R은 이러한 사전 정보를 필요하지 않아서 복잡한 연산을 하지 않으며, 단순히 이미지 쌍들을(단일 이미지도 가능) 입력으로 받아 3D 재구성을 합니다.

네트워크 구조

DUSt3R의 네트워크는 Transformer Encoder-Decoder 구조를 사용하는 신경망이며, 사전 학습된 모델(CroCo v2)을 사용합니다.

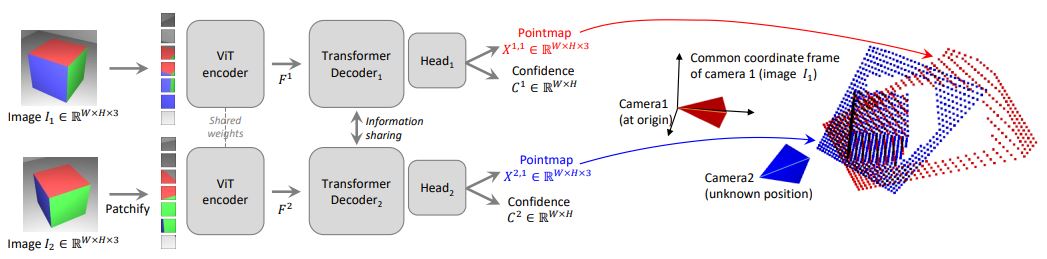두 개의 장면 이미지 $I_1, I_2$ 를 입력으로 받아서 weight를 공유하는 동일한 ViT(비전 트랜스포머) Encoder를 사용해 인코딩하여 각 이미지 특징들인 $F_1, F_2$ 를 생성합니다. (Siamese 방식)

$ F_1 = Encoder(I_1), F_2 = Encoder(I_2) $

Decoder는 CroCo v2와 비슷하게 cross attention 기능이 포함되어 있는 일반적인 트랜스포머 네트워크로 구성됩니다. 각 Decoder는 Self-Attention(각 이미지의 토큰이 동일 이미지 내의 다른 토큰을 참고), Cross-Attention(각 이미지의 토큰이 다른 이미지의 모든 토큰을 참고), MLP(Multi-Layer Perception, 최종적으로 각 토큰을 MLP에 전달하여 처리) 순서로 동작합니다. 이때, 디코더는 각 블록에서 정보가 지속적으로 공유하고 두 이미지의 정보가 통합되어 더욱 정확한 포인트 맵을 생성하도록 합니다.

$ \begin{aligned} G^1_i &= DecoderBlock^1_i(G^1_{i-1}, G^2_{i-1}) \\ G^2_i &= DecoderBlock^2_i(G^2_{i-1}, G^1_{i-1}) \end{aligned} $

위와 같은 과정이 $i = 1, … , B$ 개의 블록에 걸쳐 반복됩니다. $G^1_0 = F^1, G^2_0 = F^2$ 로 초기화합니다. 각 branch의 regression head가 decoder의 토큰들 세트를 받아 pointmap(X)과 associated confidence map(C)을 출력합니다. 이때, pointmap은 $I_1$의 좌표 프레임으로 표현됩니다.

$ \begin{aligned} X^{1,1}, C^{1,1} &= Head^1(G^1_0, ..., G^1_{B}) \\ X^{2,1}, C^{2,1} &= Head^2(G^2_0, ..., G^2_{B}) \end{aligned} $

monocular depth estimation처럼 네트워크가 생성하는 pointmap은 실제 물리적 크기와 다를 수 있습니다. (scale이 다를 수 있음)

학습 목표 (Loss)

네트워크는 loss 함수를 최소화하도록 학습합니다.

1. 3D Regression loss

3D 공간에서 regresstion이 목표입니다. 실제 포인트맵 $ \overline{X}$ 를 사용하고 유효한 픽셀 집합 D를 포함합니다.

$ \begin{aligned} loss_{regr}(v, i) = || \frac{1}{z}X^i_{v,1} - \frac{1}{\overline{z}}\overline{X}^i_{v,1} || \end{aligned} $

z는 정답과 예측값의 scale을 위한 변수이며, 각 view에 대한 depth 값으로 계산됩니다. 예측값과 정답 간의 scale ambiguity를 조절하기 위해 scale 변수 z를 사용합니다.

$ \begin{aligned} z = norm(X^{1,1}, X^{2,1}) \\ \overline{z} = norm(\overline{X}^{1,1}, \overline{X}^{2,1}) \end{aligned} $

z는 위와 같고 각각, 단순히 원점까지의 모든 유효한 지점의 평균 거리입니다.

$ \begin{aligned} norm(X^1, X^2) = \frac{1}{|D^1| + |D^2|}\sum_{v \in {1,2}}\sum_{i \in D^v}||X^v_i|| \end{aligned} $

2. Confidence-aware loss

실제 상황에서는 잘 정의되지 않은 3D 포인트가 존재할 수 있으며(하늘이나 투명한 물체와 같이), 이미지의 일부 영역은 예측하기 더 어려울 수 있습니다. 따라서, 네트워크는 각 픽셀에 대한 신뢰도를 함께 예측하도록 학습됩니다. 최종적으로 모든 유효 픽셀에 대해 Confidence-Weighted regression loss를 사용하는 것입니다.

$ \begin{aligned} L_{conf} = \sum_{v \in {1,2}}\sum_{i \in D^v}C^i_{v,1} l_{regr}(v,i) - \alpha \log C^i_{v,1} \end{aligned} $

여기서 $C^i_{v,1}$ 은 픽셀 i에 대한 신뢰도 점수이며, $\alpha$는 regularization term을 조절하는 hyper-parameter 입니다.

활용

1. Point matching (포인트 매칭)

3D pointmap의 특성을 이용해서 이미지 간의 Point Matching을 쉽게 수행할 수 있습니다. 3D pointmap 공간에서 NN(nearest neighbor) search를 통해 두 이미지의 Point Matching을 설정할 수 있습니다.

$ \begin{aligned} M_{1,2} = {(i,j)| i=NN^{1,2}_1(j) and j=NN^{2,1}_1(i)} \\ with \ NN^{n,m}_k(i) = \arg \min ||X^{n,k}_j - X^{m,k}_j|| \end{aligned} $

error를 최소화하기 위해, 일반적으로 상호 대응 $M_{1,2}$ 을 유지합니다.

2. Recovering intrinsics (내부 파라미터 추정)

pointmap $X^{1,1}$은 I_1의 좌표계에서 표현되므로, 간단한 최적화 문제를 해결하여 카메라 내부 파라미터를 추정할 수 있습니다. 이 과정에서 principal point는 중심에 가깝고 픽셀이 정사각형이라고 가정합니다.

$ \begin{aligned} f^*_1 = \arg \min\limits_{f_1} \sum^W_{i=0} \sum^H_{j=0} C^{1,1}_{i,j} ||(i', j') - f_1 \frac{X^{1,1}_{i,j,0}, X^{1,1}_{i,j,1}}{X^{1,1}_{i,j,2}} || \\ with i'=i-\frac{W}{2}, j'=j-\frac{H}{2} \end{aligned} $

3. Relative pose estimation (상대적 포즈 추정)

2D matching과 intrinsic을 복원하면 Epipolar matrix와 relative pose를 구할 수 있습니다. [링크 추가 예정]

또 다른 방법으로 Procrustes Alignment를 이용해서 다른 뷰에서 보는 3D pointmap이 동일해지도록 최적화 문제를 푸는 방법 입니다.

$ \begin{aligned} R^*, t^* = \arg \min\limits_{\sigma, R, t} \sum_i C^{1,1}_i C^{1,2}_i ||\sigma(RX^{1,1}_i + t) - X^{1,2}_i|| \end{aligned} $

이 방법은 노이즈와 outlier에 민감하므로 PnP(Perspective n Points Algorithms)를 활용한 RANSAC(Random Sample Consensus)에 의해 결과가 좌우됩니다.

4. Absolute pose estimation (절대적 포즈 추정)

Absolute pose estimation(visual localization)은 여러 방법으로 달성할 수 있습니다. 이미지 쿼리 $I_Q$ 와 2D-3D 대응이 가능한 참조 이미지 $I_B$를 사용하여 카메라 절대 위치와 방향을 추정합니다. 1) $I_Q$의 내부 파라미터를 pointmap $X_{Q,Q}$로 추정

카메라의 정확한 위치와 방향을 계산하는데 사용됩니다.

2) PnP-RANSAC 실행

$I_Q$와 $I_B$사이의 2D 대응시켜 2D-3D 대응을 생성한 다음, PnP-RANSAC을 실행

3) 상대 포즈 추정

앞서 설명한 방식으로 이미지 간 상대 포즈를 추정합니다. 그런 다음, $X_{B,B}$와 참조 이미지 $I_B$의 실제 pointmap 간의 스케일을 사용하여 포즈를 월드 좌표로 변환합니다.

이러한 과정을 통해 카메라의 절대적인 위치와 방향을 추정할 수 있습니다.

Global Alignment (전역 정렬)

소개된 네트워크는 오직 1쌍의 이미지만 다룰 수 있습니다. 이제 전체 이미지들에 대한 후처리 최적화를 소개합니다.

1. Pairwise graph

주어진 이미지들 ${I_1, I_2, … , I_N}$에 대해 연결 그래프 $G(V, E)$를 구성합니다. 여기서 N개의 이미지들은 정점 $V$를 형성하고, 각 edge $e=(n,m) \in \epsilon$ 는 $I_n$과 $I_m$과 공유하는 시각적 요소들을 나타냅니다. 모든 쌍들을 네트워크로 보내고 쌍들 간에 평균 신뢰도를 기준으로 중복을 측정한 다음 신뢰도가 낮은 쌍들을 필터링합니다.

2. Global optimization

최적화는 각 이미지 쌍에 대해 pointmap을 일관되게 정렬하여 전체 장면의 3D 구조를 복원하는 것을 목표로 합니다.

$ \begin{aligned} \chi^* = \arg \min\limits_{\chi, P, \sigma} \sum_{e \in \epsilon} \sum_{v \in e} \sum^{HW}_{i=1} C^{v,e}_i || \chi^v_i - \sigma _e P_e X^{v,e}_i || \end{aligned} $

$\chi^n$는 각 이미지 $I_n$에 대해 예측된 3D pointmap입니다. 위 식에서 $e = (n, m)$입니다. 주어진 쌍 e에 대해 동일한 rigid transformation $P_e$가 두 pointmap $X_{n,e}, X_{m,e}$를 월드 좌표계 pointmap $\chi _n, \chi _m$로 맞춥니다. 이 때, $ \sigma _e = 0, \forall e \in \varepsilon $ 인 작은 최적값을 피하기 위해 $\Pi _e \sigma _e = 1$ 적용했습니다.

3. Recovering camera parameters

이 프레임워크를 전역으로 확장시키면 모든 카메라 파라미터들을 구할 수 있습니다.

$ \begin{aligned} \chi^n_{i,j} = P^{-1}_n h (K^{-1}_n[iD^n_{i,j};jD^n{i,j};D^n_{i,j}]) \end{aligned} $

를 변환하면(하나의 카메라를 표준 카메라 핀홀 모델로 잡으면) 모든 카메라 포즈들, depthmap, 내부 파라미터들을 구할 수 있습니다.

bundle adjustment처럼 2D reprojection error를 최소화하는 것이 아니라 3D projection error를 최소화합니다. 이러한 최적화는 standard gradient descent를 통해 수행됩니다.

실험 관련

데이터 셋

이 논문에서는 Waymo, Blended MVS, Static Scenes 3D와 같이 indoor, outdoor, synthetic, real-world 등 다양한 데이터 셋들로 실험을 진행하였습니다. 이미지 쌍이 데이터 셋과 제공되지 않는 경우에는 Croco v2에 설명된 방법을 기반으로 추출합니다.

실험 세팅

1. 각 epoch마다 데이터 셋 크기 불균형을 해소하기 위해 각 데이터셋에서 동일한 수의 쌍을 무작위로 샘플링합니다.

2. 네트워크에 상대적으로 고해상도의 이미지를 입력하고자 512 픽셀 이미지를 사용합니다. 이 때, 고해상도 이미지의 높은 비용을 줄이기 위해, 먼저 $224 \times 224$ 로 네트워크를 학습한 후, 512 픽셀 이미지로 점진적으로 훈련합니다.

3. 각 batch마다 무작위로 이미지의 w, h 비를 선택하여 테스트시 다양한 이미지에 익숙해지도록 했습니다. 이미지를 원하는 종횡비로 잘라내고, 가장 큰 차원인 512 픽셀에 맞도록 크기를 조정했습니다.

4. 네트워크 구조는 Vit-Large의 encoder, ViT-Base의 decoder, DPT(ViT를 Depth Estimation에 적용) head로 구성됩니다.

5. CroCo는 MAE에서 영감을 받은 사전 훈련 패러다임으로 다양한 3D 비전 작업에서 우수한 성능을 보였기에, off-the-shelf CroCo 사전 모델 가중치로 네트워크를 초기화합니다.

평가

특정 downstream 작업에 대해 모델을 미세조정(finetuning)하지 않았습니다. 테스트 시 모든 테스트 이미지는 w, h 비율을 유지하면서 512px 크기로 조정됩니다.

unseen MegaData scene에 대한 결과입니다. 왼쪽 그림에 중앙은 depthmap, 오른쪽은 confidence map입니다.

마찬가지로 unseen data에 대한 결과입니다.

outdoor에서도 unseen data에 대해 잘 나오는 것을 확인할 수 있습니다.

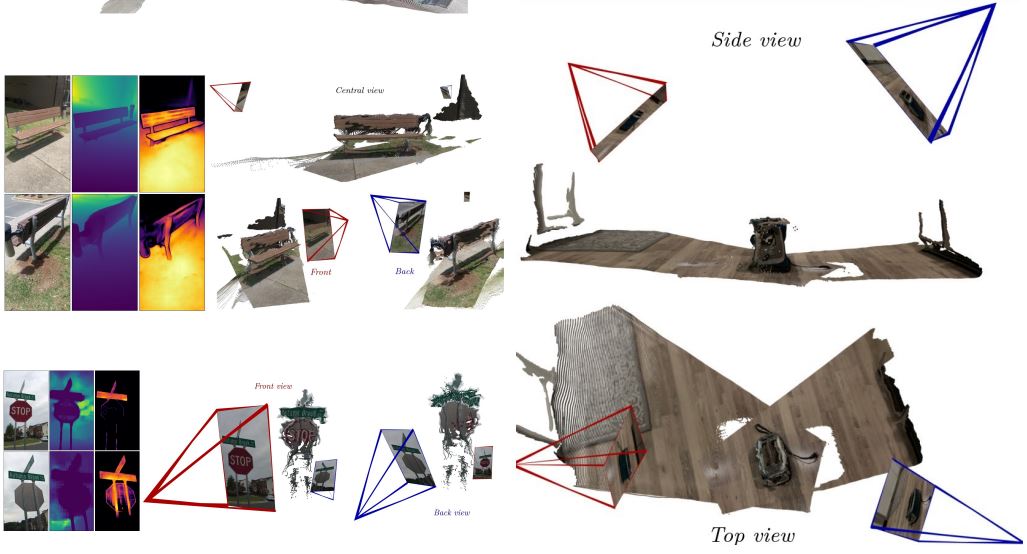거의 180도 반대쪽에서 찍힌 이미지에서도 잘 나온다는 것을 확인할 수 있습니다.

결론

DUSt3R은 정량적인 성능으로 sota는 아니지만 전통적인 방법과 달리 이미지로부터 3D reconstruction 작업을 간편하고 효율적으로 수행할 수 있는 혁신적인 접근법을 제시합니다. 이 모델은 복합한 camera calibration이나 카메라 포즈 정보 없이도 다양한 3D 비전 작업을 단일 네트워크로 통합할 수 있음을 보여줍니다.

특히, DUSt3R은 훈련 과정에서 고해상도 이미지를 점진적으로 사용하고, 다양한 w, h 비율에 익숙해질 수 있도록 random crop과 resize를 적용하여 모델의 일반화 능력을 극대화했습니다.

또한, 기존 최신 방법들과 비교하여 경쟁력 있는 성능을 보여줬으며 다양한 데이터 셋에서 높은 품질의 3D reconstruction을 수행하였습니다.

카메라 포즈 추정에 있어서도 기존의 네트워크 모델들이 성능 문제를 겪고 있었으나, DUSt3R는 이 문제를 효과적으로 해결할 수 있는 잠재력을 보여주고 있습니다. 특히, PointNet 등의 모델이 성능이 저조했던 반면, DUSt3R는 카메라 포즈 추정에서도 모델이 문제를 해결할 수 있음을 시사한다 생각합니다.

이것저것 공부하면서 관련 내용에 대해 계속 추가할 예정입니다. 궁금한 것들이나 추가 및 수정했으면 좋겠는 거 말해주시면 좋을 거 같아요. 좋은 하루 보내시길 바래요 :)