[Computer Vision] PGO(Pose Graph Optimization)에 대하여

이 글에서는 PGO(Pose Graph Optimization)가 무엇인지 간단하게 설명하고, Computer Vision에서 언제 어떻게 쓰이는지 예시와 함께 다룰 예정입니다. (본인 공부 및 기록용)😁

PGO(Pose Graph Optimization)란?

PGO(Pose Graph Optimization)는 로봇 공학과 컴퓨터 비전에서 중요한 역할을 하는 “최적화 기법”입니다. 주로 SLAM (Simultaneous Localization and Mapping) 시스템에서 사용되며, “로봇이 환경을 탐색하면서 자신의 위치를 정확하게 추정”하고, 동시에 “주위 환경의 지도를 생성”하는 데 필수적인 요소입니다.

기본 개념

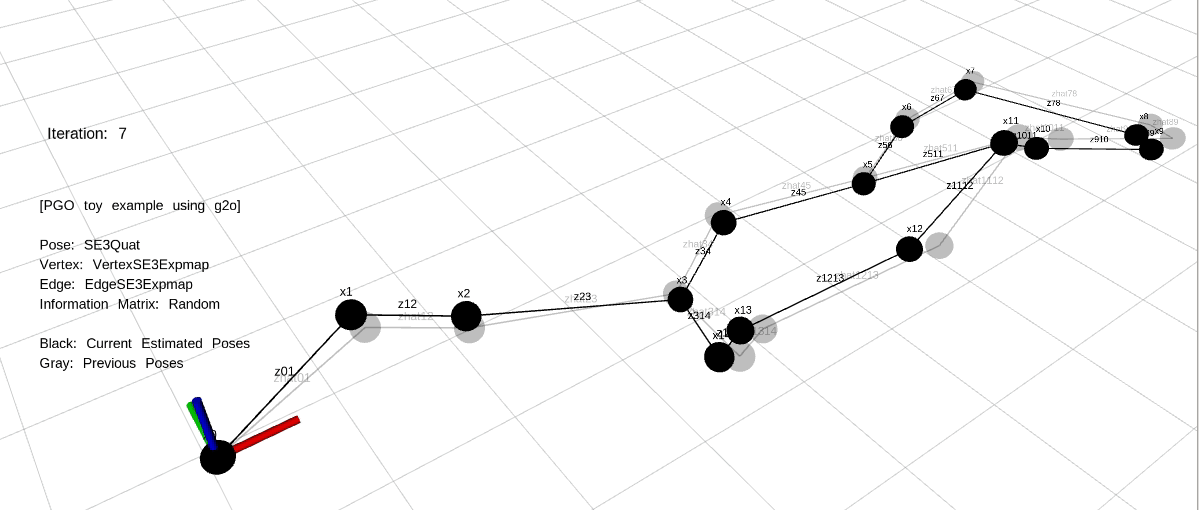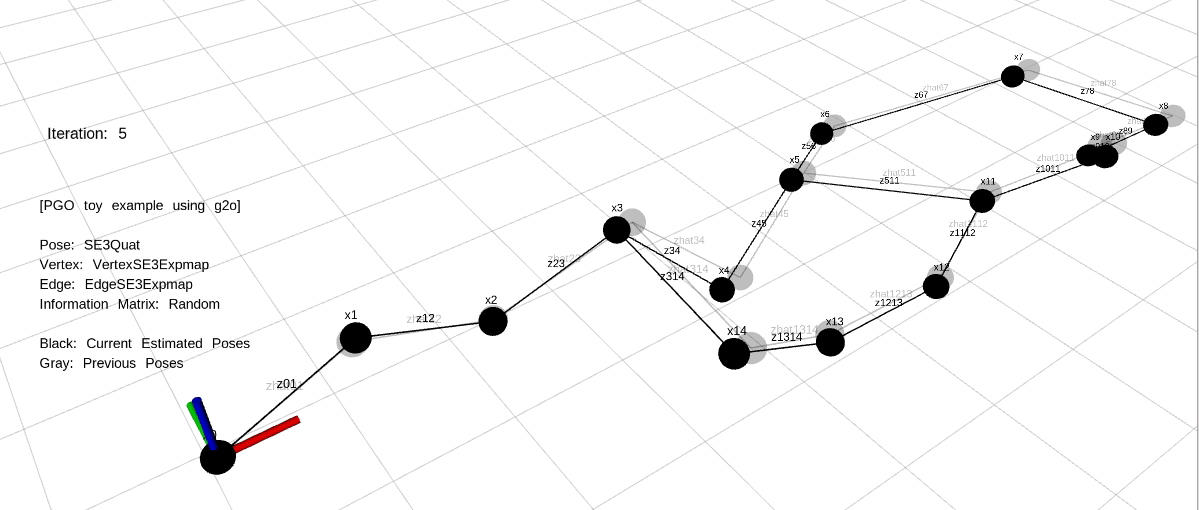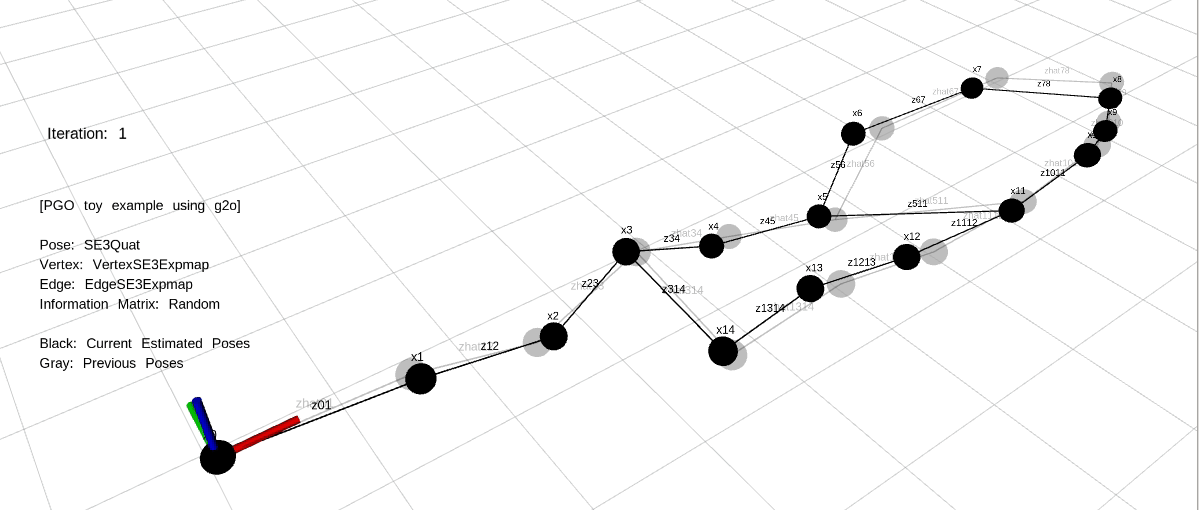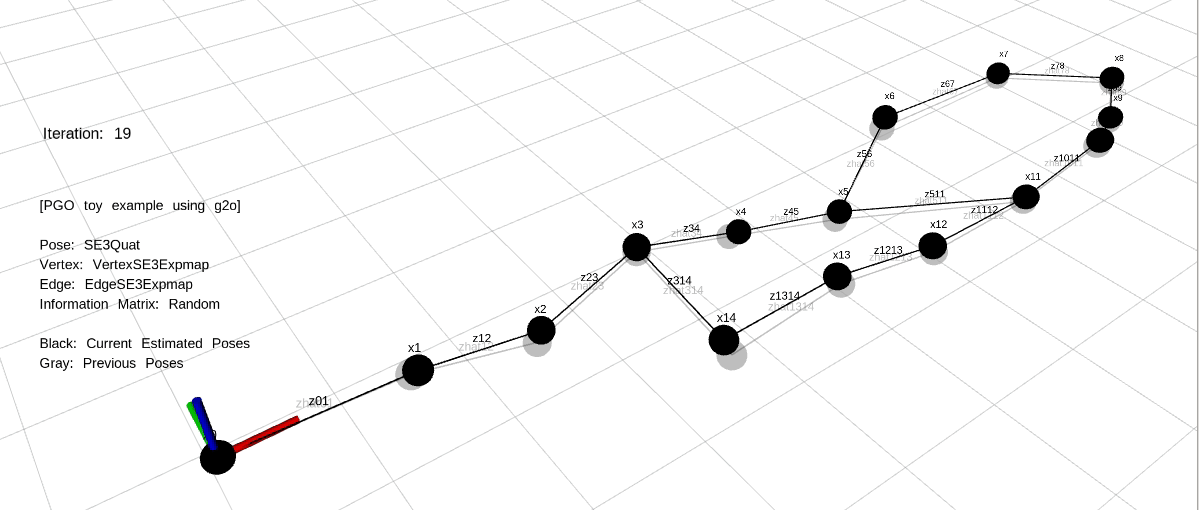
PGO는 로봇의 위치(포즈)를 노드로, 이 위치들 간의 상대적인 관계를 엣지로 나타내는 그래프를 최적화하는 과정입니다. 각 엣지는 두 포즈 사이의 상대적인 변환을 나타내며, 이 변환은 일반적으로 센서 데이터(예: LiDAR, 카메라, IMU)에서 얻어집니다.

PGO와 BA(Bundle Adjustment) 차이

두 기법은 매우 유사한 최적화 원리를 사용하지만, “PGO는 위치 추정”에, “BA는 이미지와 3D 포인트의 일관성 유지”에 목표를 두고 있습니다. 요약하자면 PGO는 카메라/로봇의 포즈를 최적화, BA는 카메라 포즈와 3D 포인트 둘 다 최적화합니다.

PGO 주요 요소

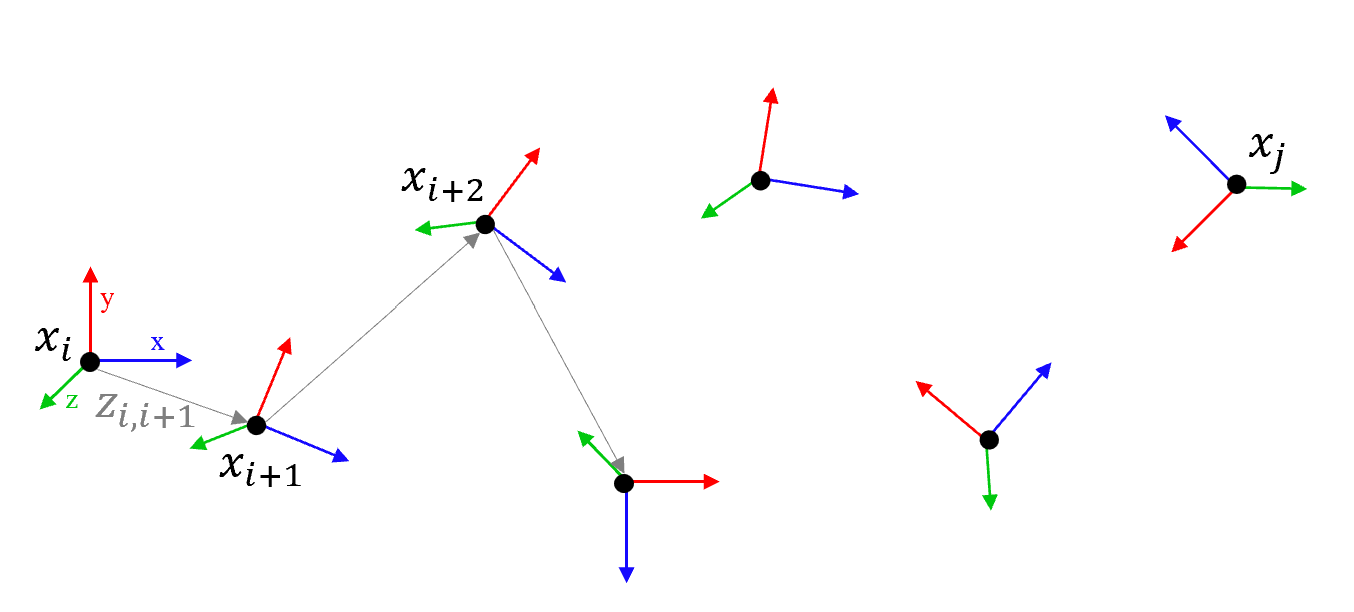
1. 노드 (Nodes)

각 노드는 로봇/카메라의 특정 시점에서의 위치와 방향을 나타냅니다.(카메라 외부 파라미터와 동일합니다.) 포즈는 일반적으로 2D 공간에서는 $(x, y, \theta)$, 3D 공간에서는 $(x, y, z, roll, pitch, yaw)$로 표현됩니다.

\[\text{(Node)} \ \mathbf{x}_i = \begin{bmatrix} \mathbf{R}_i & \mathbf{t}_i \\ \mathbf{0}^\top & 1 \end{bmatrix} \in \mathbb{R}^{4 \times 4}\]

2. 엣지 (Edges)

각 엣지는 두 노드 간의 상대적인 변환을 나타냅니다. 이 변환은 로봇이 두 위치 간 이동할 때 측정된 변위와 회전을 기반으로 합니다. (두 카메라 외부 파라미터의 상대적 차이라 보시면 됩니다.)

\[\text{(Edge)} \ \mathbf{z}_{ij} = \begin{bmatrix} \mathbf{R}_{ij} & \mathbf{t}_{ij} \\ \mathbf{0}^\top & 1 \end{bmatrix} \in \mathbb{R}^{4 \times 4}\]

3. 측정값 (Measurements)

센서 데이터를 통해 얻은 두 노드 간의 상대적인 위치 변환 값으로, 이 값들이 그래프의 엣지를 구성합니다. 측정값에는 노이즈가 포함될 수 있습니다.

측정값 예시

로봇이 이동하면서 센서를 통해 현재 위치와 다음 위치 간의 변위를 측정합니다. 이 변위는 이동거리와 회전 각도로 표현됩니다.

• 3차원 공간: $(\Delta x, \Delta y, \Delta z, \Delta roll, \Delta pitch, \Delta yaw)$

4. 오차 함수 (Error Function)

각 엣지에 대해 “예상되는 변환”과 “실제 측정된 변환” 간의 “차이”를 나타내는 함수입니다. PGO의 목표는 이 오차 함수를 최소화하는 것입니다. 로봇이 A 지점에서 B 지점으로 이동했다고 가정해봅시다. 센서를 통해 얻은 측정값은 $(\Delta x_m, \Delta y_m, \Delta \theta _m)$ 입니다. 하지만 실제로는 $(\Delta x_e, \Delta y_e, \Delta \theta _e)$ 일 수 있습니다. 오차 함수는 이 두 값 간의 차이를 계산하여 나타냅니다.

유클리드 거리 Euclidean Distance

유클리드 거리는 많은 사람들이 흔히 아는 두 점 사이의 직선 거리를 계산하는 방법입니다. 88PGO에서는 예상되는 위치와 실제 측정된 위치 간의 차이를 계산88할 때 유클리드 거리가 사용됩니다.

$E = \sqrt{(\Delta x_e - \Delta x_m)^2 + (\Delta y_e - \Delta y_m)^2 + (\Delta \theta _e - \Delta \theta _m)^2}$

$\Delta x_e, \Delta y_e, \Delta \theta _e$ : 예상된 위치와 방향의 좌표

$\Delta x_m, \Delta y_m, \Delta \theta _m$ : 실제 측정된 위치와 방향의 좌표

기하학적 오차 Geometric Error

기하학적 오차는 로봇의 위치와 방향을 모두 고려하여 오차를 계산합니다. 이는 보통 행렬 형태로 표현됩니다. $E = \Vert T^{-1}_e T_m - I \Vert$

$T_e$ : 예상된 변환 행렬, $T_m$ : 측정된 변환 행렬, $I$ : 단위 행렬, $T^{-1}_eT_m$: 예상 변환을 실제 변환으로 변환한 결과

휴버 손실 함수 Huber Loss Function

Huber 손실 함수는 유클리드 거리와 절대 오차를 결합하여 큰 오차와 작은 오차를 다르게 처리합니다. 작은 오차는 유클리드 거리로 계산하고, 큰 오차는 절대값으로 계산하여 이상치에 덜 민감하게 반응합니다.

$ E = \begin{cases} \frac{1}{2}(z_{ij} - h(x_i, x_j))^2 & \text{if } |z_{ij} - h(x_i, x_j)| \leq \delta \newline \delta \cdot (|z_{ij} - h(x_i, x_j)| - \frac{1}{2}\delta) & \text{otherwise} \end{cases} $

$z_{ij}$: 실제 측정값, $h(x_i, x_j)$: 예상값, $\delta$: 오차의 임계값

루프 클로징 오차 Loop Closure Error

루프 클로징은 로봇이 이전에 방문한 장소를 다시 방문할 때 발생하는 오차입니다. 이를 최소화하여 경로의 일관성을 유지합니다.

$E = \sum_{i,j}{\Vert T_{ij} - (T^{-1}_i T_j) \Vert} $

여기서 $T_i$와 $T_j$는 각각 i 번째와 j 번째 노드의 포즈를 나타내고, $T_{ij}$는 i와 j 사이의 상대 변환입니다.

가우시안 노이즈 모델 Gaussian Noise Model

측정값에 포함된 노이즈를 가우시안 분포로 모델링하여 오차 함수를 구성합니다. 이는 측정값의 불확실성을 반영합니다.

$ E = \frac{1}{\sigma \sqrt{2\pi}} \exp{\left(-\frac{(x - \mu)^2}{2\sigma^2}\right)} $

여기서 $\mu$는 평균값, $\sigma$는 표준편차, $x$는 측정값을 나타냅니다.

잔차 최소화 Residual Minimization

잔차 최소화는 측정값과 예측값 간의 차이인 잔차를 최소화하는 방법입니다. 이는 보통 최소자승법(Least Squares Method)을 사용하여 구현됩니다.

$ E = \sum_{i=1}^{n} (y_i - f(x_i))^2 $

여기서 $y_i$는 실제 측정값, $f(x_i)$는 예측값을 나타내며, n은 데이터 포인트의 수입니다.

PGO 작동 원리

1. 그래프 구성

PGO에서 그래프는 노드와 엣지로 구성됩니다. 노드는 로봇의 위치(포즈)를 나타내며, 엣지는 두 위치 간의 상대 변환(측정값)을 나타냅니다. 이를 통해 로봇의 이동 경로를 그래프로 모델링할 수 있습니다.

• 노드(Node): 로봇의 특정 시간에 대한 위치와 방향을 나타냅니다. 보통 $x, y, \theta$ 형태로 표현됩니다.
• 엣지(Edge): 두 노드 간의 상대적인 위치 변화를 나타냅니다. 이는 센서 데이터를 기반으로 측정된 값입니다.

2. 오차 함수 정의

오차 함수는 예상되는 측정값과 실제 측정값 간의 차이를 계산하여 정의됩니다. 이를 통해 그래프의 노드가 실제 환경과 얼마나 일치하는지를 평가할 수 있습니다. 위의 오차함수들을 사용합니다.

3. 최적화 알고리즘

오차 함수를 최소화하기 위해 다양한 최적화 알고리즘이 사용됩니다. 일반적으로 사용되는 알고리즘으로는 가우스-뉴턴 알고리즘, 르벤베르그-마르콰르트 알고리즘, 그리고 그래디언트 디센트 방법이 있습니다.

가우스-뉴턴(Gauss-Newton) 알고리즘:

이 알고리즘은 비선형 최소제곱 문제를 해결하기 위해 사용되며, 오차 함수를 반복적으로 선형화하여 최적화합니다.

$ \mathbf{x}_{k+1} = \mathbf{x}_k - (\mathbf{J}_k^T \mathbf{J}_k)^{-1} \mathbf{J}_k^T \mathbf{r}_k $

여기서 $\mathbf{J}_k$는 오차 함수의 야코비안 행렬, $\mathbf{r}_k$는 잔차 벡터입니다.

르벤베르그-마르콰르트(Levenberg-Marquardt) 알고리즘:

가우스-뉴턴 알고리즘과 그래디언트 디센트 방법의 혼합 형태로, 수렴 속도를 높이고 최적화를 안정화합니다.

$ \mathbf{x}_{k+1} = \mathbf{x}_k - (\mathbf{J}_k^T \mathbf{J}_k + \lambda \mathbf{I})^{-1} \mathbf{J}_k^T \mathbf{r}_k $

여기서 $\lambda$는 정규화 파라미터, $\mathbf{I}$는 단위 행렬입니다.

그래디언트 디센트 방법(gradient descent):

오차 함수의 그래디언트를 계산하여, 최적의 값을 찾을 때까지 반복적으로 갱신합니다.

$ \mathbf{x}_{k+1} = \mathbf{x}_k - \alpha \nabla E(\mathbf{x}_k) $

여기서 $\alpha$는 학습률, $\nabla E(\mathbf{x}_k)$는 오차 함수의 그래디언트입니다.

PGO 활용

1. 로봇 내비게이션

   PGO는 로봇이 주어진 경로를 정확히 따라가고, 장애물을 피하며 목적지에 도달할 수 있도록 도와줍니다. SLAM (Simultaneous Localization and Mapping) 알고리즘의 핵심 요소로 사용됩니다.

2. 자율 주행 차량

   자율 주행 차량은 정확한 위치 추정과 경로 계획을 위해 PGO를 사용합니다. 이를 통해 안전한 주행 경로를 계획하고, 도로 상황에 맞게 차량을 제어합니다.

3. AR/VR 시스템

   AR (Augmented Reality) 및 VR (Virtual Reality) 시스템에서는 사용자의 움직임을 추적하여, 가상 환경과의 상호작용을 원활하게 합니다. PGO를 통해 사용자의 위치를 정확히 추정하고, 가상 객체를 적절한 위치에 배치할 수 있습니다.

이것저것 공부하면서 PGO(Pose Graph Optimization)에 대해 새로 알게 되는 내용은 계속 추가할 예정입니다. 궁금한 것들이나 추가 및 수정했으면 좋겠는 거 말해주시면 좋을 거 같아요. 좋은 하루 보내시길 바래요 :)